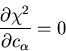
In simple cases, the problem can be solved analytically. For example the fitting of a set of points (xi,yi) to the curve:-
Then
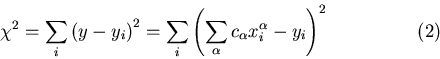
and
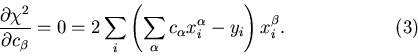
So
These are just a set of linear simultaneous equations in
Sometimes the problem is not so simple; either
![]() can only be calculated numerically or it is
not linear in
can only be calculated numerically or it is
not linear in
![]() .
In such cases an iterative numerical approach can
be used. The first step is to find some approximate solution
and then to determine the first and second derivatives of
.
In such cases an iterative numerical approach can
be used. The first step is to find some approximate solution
and then to determine the first and second derivatives of ![]() (numerically if necessary) at that point to find a better solution.
(numerically if necessary) at that point to find a better solution.
Suppose
![]() is an approximate solution, we seek a better
solution
is an approximate solution, we seek a better
solution
and assume that it is not too far away, so that we can write
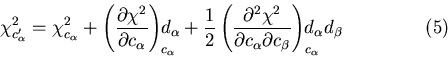
If
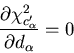
so
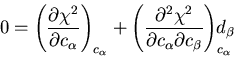
i.e.
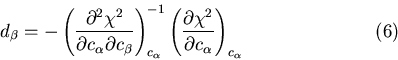
Hence